Let's Count!

For the first post, let’s talk about something so innate to our intuition, that we might as well call it… natural. You guessed it, today we’ll talk about natural numbers and the rather odd notions surrounding them.

The set of all natural numbers, $\mathbb{N} = \{0, 1, 2, …\}$, of course, goes on forever. If you give me a natural number, I can always produce the next one by adding $1$. And yet, each natural number itself is finite. But what about a number with an infinite number of $9$’s (something like $99999…$)? That, by the definition of natural numbers, is not one: a natural number must have a finite number of digits. The moral here is that you can have an infinite number things, each of which itself is finite (contrast: the six infinity stones). This is an idea that will come up multiple times in this article.

With that out of the way, let’s take a closer look at the infinity in front of us: the number of natural numbers. This cardinality of the set of natural numbers is called (defined to be) aleph null:

Since we have already established that all natural numbers are finite, our $\aleph_0$ is definitely not among them. In fact, is greater than all of them. But what about the cardinalities of other infinite sets? We defined $\aleph_0$ to be the cardinality of the natural numbers, but can we simply assign the same cardinality to other infinite sets like the set of all even numbers or the set of all real numbers?

Cardinalities

To answer these questions, we examine the concept of cardinality itself, which seems pretty intuitive, and it is most of the times. Given a finite set, we simply count the number of things in it, and that gives us the cardinality in the form of a natural number. As long as they reside within the realms of natural numbers, it’s trivial to compare and contrast different cardinalities. But what happens when cardinalities don’t belong to the natural numbers, like in the case of the set of all natural numbers or the set of all real numbers? Can we still cook up some sensible relationships among such cardinalities?

One key observation is that two finite sets have an equal cardinality if and only if there exists a bijective mapping from one set to another, that is, there exists a mapping such that each element of the first set maps to a unique element of the second, and all the elements of the second set are exhausted. We can extend this observations to infinite sets without offending our sensibilities too much. It is reasonable to say that two infinite sets have the same cardinality if there exists a bijective mapping between them. In a similar vein, the existence of an injective mapping implies a $\leq$ relationship between the cardinalities, and the existence of a surjective mapping implies a $\geq$ relationship. These observations empower us to ask the question: Can we find an infinite set that has a cardinality other than $\aleph_0$?

Countability

Before we answer that lingering question, let us probe the sets that do have $\aleph_0$ as their cardinality. For such sets, there exists a bijection from $\mathbb{N}$ into them, which is equivalent to saying that there’s a way to order these sets and assign a natural number (and therefore finite) “rank” to each of their elements. This trivially establishes the fact that $\aleph_0$ is the smallest possible infinity. After all, an infinite subset of a set with $\aleph_0$ as its cardinality can still be ranked by natural numbers.

Say, we want to talk about a set formed by the union of the set of all the natural numbers and the set of three cats:

An ordering that doesn’t help us in our quest to prove countability is

In this particular ordering, where all the natural numbers occur before all the cats, none of the cats have a finite, natural number rank associated with them. In fact, the ordering has an ordinality of $\omega + 3$, where $\omega$ is the ordinal equivalent of $\aleph_0$. But let us not worry about ordinals for now. A more suitable ordering would be

In this case, the three cats get a rank of 0, 1 and 2, and each natural number $n$ gets a rank of $n + 3$ satisfying the requirement for countability.

What if we have a countably infinite number of cats instead of just three? Once again, placing all the natural numbers before all the cats (or even the other way round this time) doesn’t work. We can, however, interleave the natural numbers and the cats:

proving that this new set is still countable. We can trivially extend this result to the union of any finite number of countable sets.

Let’s look at one more example before we move onto a much more general result. Let’s talk about all the possible pairs of natural numbers, that is: $S = \{(x, y): x, y \in \mathbb{N}\}$. Again, an ordering that doesn’t work is

because it doesn’t assign a finite, natural number rank to pairs that don’t have $0$ as their first element. Instead, we can “linearize” the set of pairs by sweeping diagonally like so:

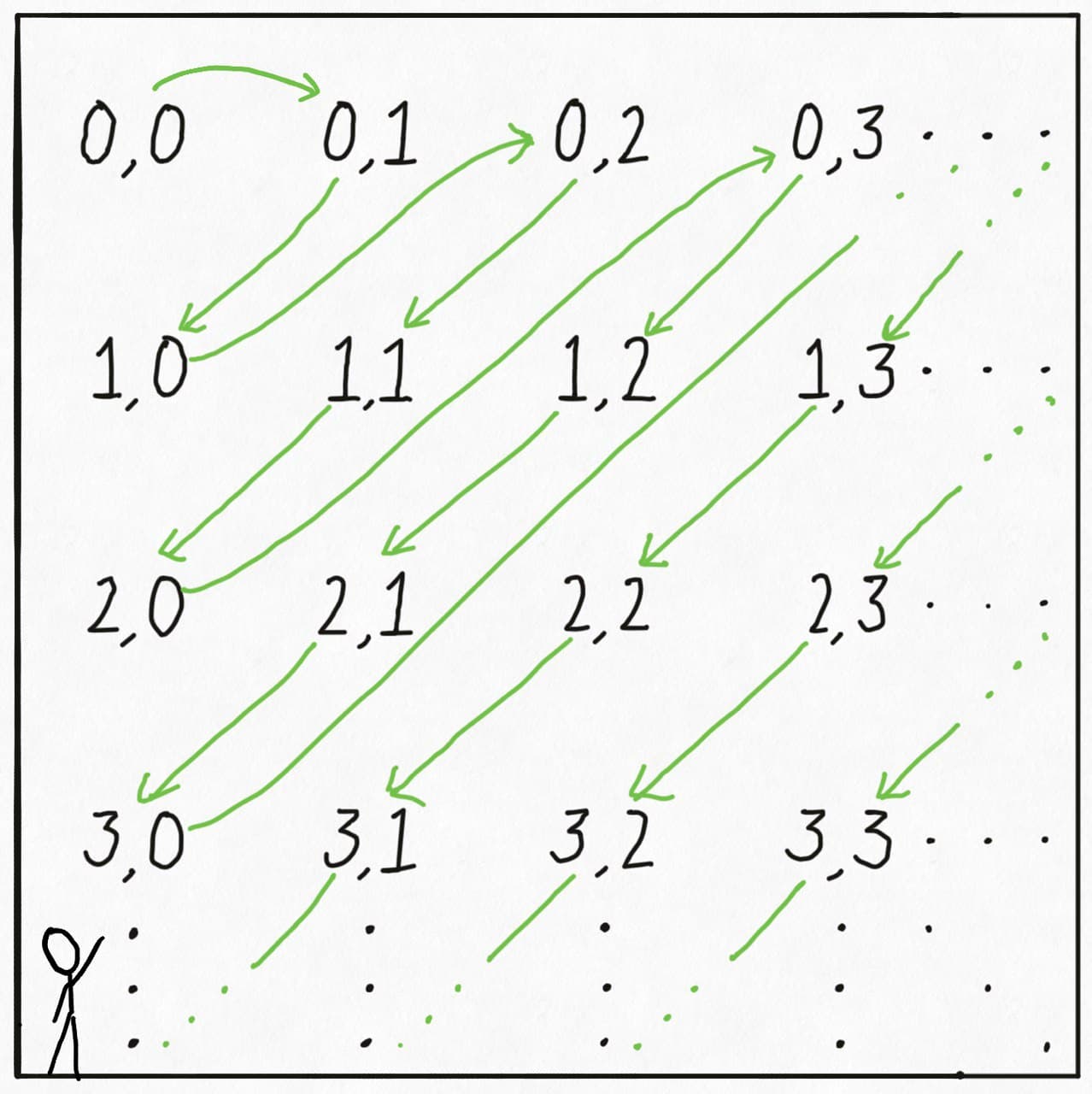
Under this “diagonal sweep” ordering, if you give me a pair of natural numbers, I will eventually reach it in a finite number of steps, proving that pairs of natural numbers are countable. Sure, the number of steps grows quadratically with respect to either dimension, but for no pair does it become infinite. Since an $n$-tuple (where $n$ is finite) can be represented as a nested pair (for instance, a triple $(x, y, z)$ can be represented as $(x, (y, z))$), we can extend this result to arbitrary $n$-tuples.

Moreover, since by definition rational numbers are of the form $\frac{p}{q}$ for an integer $p$ and a non-zero integer $q$, they can be expressed as pairs of integers which are themselves countable, ergo the rationals are countable as well (we can skip the pairs which have $\gcd(\lvert p\rvert, \lvert q \rvert) \neq 1$ when doing our diagonal dance).

In a similar vein, if we have a countably infinite number of sets each of which is itself countably infinite, we can map each individual element to a pair of natural numbers where the first element represents the rank of the set containing the element and the second one represents the rank of the element within the set (again, we can ignore the common elements when drawing our diagonals).

The formal proof for this does, however, requires the famous axiom of choice. Long story short, proofs for statements must themselves be finite strings and without using the axiom of choice the proof for the statement “A countably-infinite union of countably-infinite sets is countable” becomes infinite in size.

Finally, this ordering scheme seems tediously forced, and the idea in the next section is much more satisfying. But it is often used to “linearize” $n$-dimensional countable infinities (say, if you want to simulate a countably infinite number of Turing machines on a single one) so it’s nice to know.

Binary strings

Let us move away from the specific examples and look at something a bit more general: finite binary strings. Let’s set the scene. A finite binary string is a sequence of 0’s and 1’s with a finite but arbitrarily large length. Of course, the set of such strings is infinite (recall how there can be an infinite number of finite things). The empty string, which we shall christen $\epsilon$, is also a part of this set. If we could somehow argue that this set is countable, we could conclude that a set is countable if and only if each of its element can be encoded as a unique, finite, binary string. So how do we go about this?

The first possible ordering that comes to mind is the good old alphabetical ordering, and it should be quickly discarded, for there are an infinite number of strings that start with $0$ and the strings that start with a $1$ will never get a chance. The programmer in us may advocate interpreting the strings as binary numbers in an ascending order, maybe placing $\epsilon$ before everything else. Unfortunately, this doesn’t work either: $10_2, 010_2, 0010_2, 00010_2, …$ all represent $2_{10}$. Instead, we must use a clever trick to establish the bijection.

A bijective number system

As we saw in the last section, the leading zeros prove to be a major hindrance in our quest to find a bijective mapping between the set of finite binary strings and the natural numbers. It turns out that the most natural solution to this problem maintains the base-2 semantics but involves doing away with zero altogether and instead working with the alphabet $\Sigma = \{1, 2\}$. After all, you can’t have leading zeros if you don’t allow any zeros.

But what about the non-leading zeros? How do we compensate for them? We do this by “smearing” the higher powers of two across the lower ones until we have covered all the zeros. The digit $2$ is essential for this smearing operation. An illustrated example:

The powers of two which had non-leading zeros against them in the original binary string borrow from the higher powers, potentially introducing the digit $2$ while doing so. This process is repeated until no more zeros remain.

Finally, we use the empty string $\epsilon$ to represent the natural number $0$, thus completing the bijection. This clever bijection gives us the much coveted result: the set of all finite binary strings is countable. As mentioned previously, a corollary is that if we have a set, and we have an encoding which maps each element of the set to a unique finite string (need not be binary, since any $n$-ary string can be converted to a binary string), then that set is countable. For example, the set of all rational numbers is countable because we can represent them as the string “$(p, q)$” for two integers $p$ and $q$. The same goes for the set of all possible Python programs that you can write (or equivalently the set of all Turing machines), the set of all possible works of fiction, the set of all videos that you can play on your computer and the set of everything that can be represented in the English language!

Uncountability

This brings us back to the overarching question: “Are there sets that are not countable?” The more astute reader would’ve guessed the answer to be a “yes” given the title of this section. To finally answer this question, let’s shift our attention to the set of all infinite binary strings. An infinite binary string $s$ maps all natural numbers to either a $0$ or a $1$ such that we can get the $n$-th character as $s[n]$ for any natural number $n$. It’s not immediately apparent how we can go about formulating an ordering to prove that this set is countable. It’s even more opaque how we can go about proving uncountability, for which we need to show that none of the possible orderings work. Enter Georg Cantor and his ingenious diagonal argument.

The argument goes like this: you give me any ordering of these strings that you claim assigns a natural number rank to each of them, and I will construct an infinite string that does not appear anywhere in your ordering, proving that your claim is dishonest and brings shame upon your family. To construct this magical string given your ordering, I set the $n$th character of the string to be the bit-complement of the $n$th character of the $n$th string in your ordering. So if your ordering looks like $10010…, 01001…, 11001…, 00110…, …$, my string will look like $0010…$

For all natural numbers $n$, this constructed string differs from the $n$th string in your ordering at position $n$. Therefore, there is no string in your list that is exactly equal to my constructed string. Since I can do it for any possible list that you can throw at me, I can conclude that no such ordering is possible, demonstrating the uncountability of this set.

If we were to extend exponentiation to infinite cardinals, we could write the cardinality of this set as $2^{\aleph_0} > \aleph_0$. This number is also called the cardinality of the continuum ($\mathfrak{c}$) for reasons that will be elucidated momentarily, and beth one ($\beth_{1}$). Why is it not called $\aleph_1$? It so happens that $\aleph_1$ is defined to be the second smallest infinite cardinality and whether $\mathfrak{c}$ is equal to it or not is complicated.

Now that we have one uncountable set at hand, we can look for other uncountable sets by trying to cook up bijections against infinite binary strings. One such set that comes to mind is the set of all the subsets of natural numbers. We can represent a (possibly infinite) subset of natural numbers as an infinite binary string, with a $1$ at the $n$th position representing the presence of the natural number $n$ in the subset and a $0$ representing the absence. This bijection tells us that the set of all subsets (the power set) of natural numbers is also uncountable.

Finally, we can convert an infinite binary string $s$ to a real number in $[0, 1]$ by interpreting it as a the real number represented by $0.[s]_2$. Note how the interval is closed at $1$, since $0.1111…_2$ is exactly equal to $1$. We can then construct a bijection from $[0, 1]$ to all real numbers (it’s much easier to get a bijection from $(0, 1)$ to $\mathbb R$; using $[0, 1]$ requires a bit more work). This finally proves that the set of all real numbers is uncountable as well and has a cardinality of $\mathfrak{c}$. This leads to a surprising, somewhat doleful realization that the fraction of real numbers that we can express in words or equations or write computer programs to calculate is insignificant, an aptly representative notion to serve as the conclusion to this article.

Citation

1
2
3
4
5
6
7

@online{dabral2020,
  author = {Dabral, Tanmaya Shekhar},
  title = {Let's Count!},
  date = {2020-04-21},
  url = {https://www.vanillabug.com/posts/lets-count/},
  langid = {en}
}

Or:

1

Dabral, T. S. (2020, April 21). Let’s Count! Retrieved from https://www.vanillabug.com/posts/lets-count/